Lý thuyết danh mục đầu tư Markowitz (MPT)

“A good portfolio is more than a long list of good stocks and bonds. It is a balanced whole, providing the investor with protections and opportunities with respect to a wide range of contingencies.”

Năm 1952, Harry Markowitz công bố Lý thuyết danh mục đầu tư của mình đưa ra phương pháp định lượng giúp tối ưu hóa danh mục đầu tư bằng cách cân bằng rủi ro và lợi nhuận. Lý thuyết này đã thay đổi thị trường tài chính, đặt nền móng cho đầu tư định lượng và nhiều lý thuyết tài chính hiện đại bây giờ.

Modern Portfolio Theory

Lý thuyết danh mục đầu tư Markowitz hay còn được gọi là Lý danh mục đầu tư hiện đại (Modern Portfolio Theory - MPT) tập trung vào việc tìm kiếm danh mục có lợi nhuận kỳ vọng cao nhất cho một mức rủi ro nhất định, hoặc rủi ro thấp nhất cho một mức lợi nhuận kỳ vọng nhất định. MPT dựa trên các ước tính về lợi nhuận kỳ vọng và ma trận hiệp phương sai của các tài sản. Thay vì tập trung vào việc tìm kiếm tài sản có lợi suất cao nhất, MPT đề xuất rằng nhà đầu tư nên đa dạng hóa danh mục để giảm biến động.

Rủi ro trong mô hình được giả định và đo lường rất cụ thể bởi vì đây là điểm mấu chốt để có thể định lượng và tối ưu hóa danh mục đầu tư. Rủi ro trong mô hình được đo lường bằng Phương sai hoặc Độ lệch chuẩn. Phương sai/độ lệch chuẩn là một thước đo thống kê cho thấy mức độ phân tán của các kết quả lợi nhuận có thể xảy ra xung quanh giá trị lợi nhuận kỳ vọng. Một phương sai hoặc độ lệch chuẩn càng lớn, có nghĩa là lợi nhuận của tài sản hoặc danh mục càng biến động và do đó, càng rủi ro.  

Với một danh mục đầu tư có N tài sản, rủi ro của danh mục được tính bằng công thức:

hay còn được viết dạng rút gọn:

Trong đó: 

• sigma bình phương là phương sai của danh mục (P) hay của tài sản (i, N)
• omega (w) là tỷ trọng đầu tư của tài sản tương ứng
• Cov(Ri, Rj) là hiệp phương sai của giữa lợi nhuận của tài sản tương ứng
• w là vector cột chứa các tỷ trọng đầu tư của các tài sản
• wT là chuyển vị của vector w
• Sigma là ma trận hiệp phương sai (covariance matrix) của các tài sản, có kích thước N×N. Các phần tử trên đường chéo chính của ma trận này là phương sai của từng tài sản (sigma bình phương​), và các phần tử ngoài đường chéo là hiệp phương sai giữa các cặp tài sản Cov(Ri, Rj). 

Ứng với từng tỷ trọng của tài sản trong danh mục, chúng ta có từng rủi ro (được tính bởi công thức ở trên) và lợi nhuận kỳ vọng (được tính bằng lợi nhuận kỳ vọng của từng tài sản nhân với tỷ trọng) tương ứng. Nhà đầu tư sẽ lựa chọn danh mục nằm trên đường biên hiệu quả (efficient frontier), một tập hợp các danh mục đầu tư tối ưu mang lại lợi suất cao nhất với mức rủi ro nhất định.

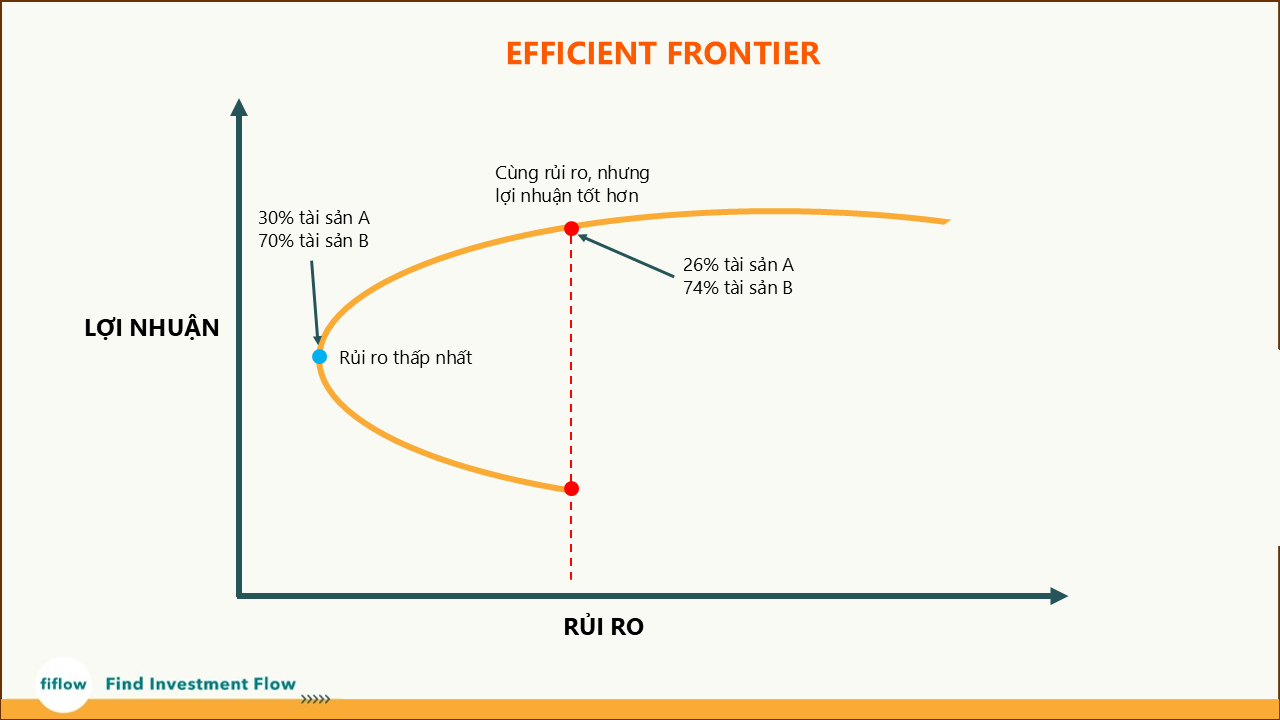
Nếu bạn đã học lý thuyết này từ các giáo trình tài chính ở giảng đường, trung tâm tài chính, bạn có thể sẽ được lấy ví dụ với 2 tài sản vì việc tính toán dễ dàng với ít tài sản. Thường chúng ta sẽ có được một đường biên hiệu quả giống với hình ở trên. 

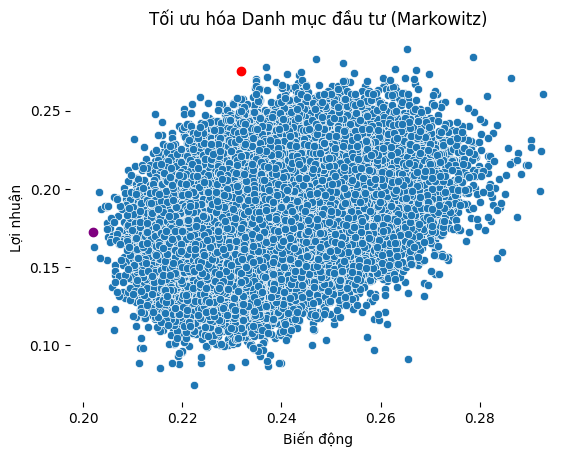
Việc tính toán nhiều tài sản và với dữ liệu lớn đòi hỏi phải có sức mạnh của máy tính. Ví dụ như ảnh bên dưới là Fiflow tính toán rủi ro và lợi nhuận một danh mục với 10 cổ phiếu. Sử dụng thuật toán và máy tính để thực hiện sẽ tiết kiệm được rất nhiều thời gian so với con người làm.

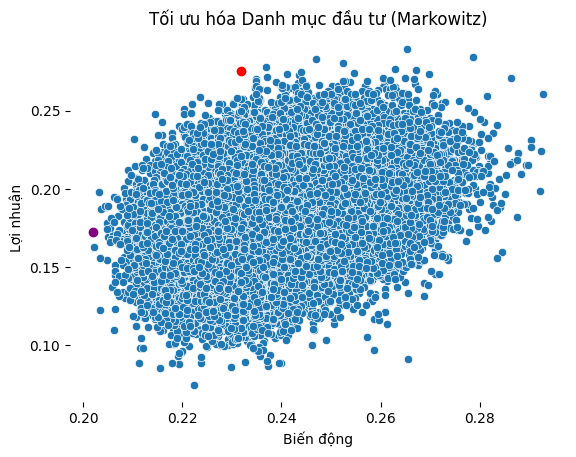
Ứng dụng mô hình Markowitz

Tối ưu hóa danh mục đầu tư

Trong giao dịch định lượng, các quỹ đầu tư sử dụng mô hình Markowitz để xây dựng danh mục tối ưu, thay vì chỉ tập trung vào một số cổ phiếu riêng lẻ. Bằng cách xác định sự tương quan giữa các tài sản, thuật toán có thể phân bổ vốn hợp lý nhằm giảm thiểu biến động thị trường.

Ứng dụng trong thuật toán giao dịch

Mô hình Markowitz cũng được sử dụng để phát triển các chiến lược giao dịch định lượng dựa trên việc tối ưu hóa rủi ro/lợi nhuận. Một số thuật toán phổ biến bao gồm:

• Thuật toán tái cân bằng danh mục: Điều chỉnh tỷ trọng tài sản trong danh mục dựa trên dữ liệu thị trường.
• Quản lý rủi ro động: Định lượng mức độ rủi ro có thể chấp nhận để tự động điều chỉnh vị thế giao dịch.
• Arbitrage giữa các danh mục đầu tư: So sánh hiệu quả của danh mục hiện tại với đường biên hiệu quả để xác định điểm mua bán tối ưu.

Kết hợp với Machine Learning

Trong các quỹ đầu tư định lượng hiện đại, mô hình Markowitz được kết hợp với Machine Learning để tự động tìm danh mục tối ưu dựa trên dữ liệu lịch sử và dự đoán xu hướng thị trường. Điều này giúp các nhà đầu tư không chỉ giảm rủi ro mà còn tối ưu hóa lợi suất theo thời gian.

Hướng dẫn chạy mô hình bằng Python

Bạn có thể học các xây dựng mô hình Markowitz bằng Python thông qua video youtube này. Trong video này, Fiflow hướng dẫn bạn viết code từng bước để xây dựng mô hình.

Hạn chế của mô hình

Markowitz có những hạn chế thực tế, đặc biệt là sự nhạy cảm cao với các ước tính đầu vào (lợi nhuận kỳ vọng và hiệp phương sai), vốn thường được ước tính từ dữ liệu lịch sử và có thể không phản ánh chính xác tương lai. Những giả định của mô hình cũng chính là hạn chế như giả định rằng thị trường hiệu quả và không có yếu tố phi lý trí.

Để khắc phục những hạn chế này, các nhà giao dịch định lượng thường kết hợp MPT với các mô hình khác như Bayesian Optimization hoặc Factor Models để có kết quả chính xác hơn. 

Dù có những hạn chế của mô hình, việc nắm rõ MPT là điều cần thiết cho những ai muốn nghiên cứu sâu hơn về việc quản trị danh mục và tài chính định lượng. Hy vọng thông qua bài này, bạn có thể hiểu hơn công việc của các nhà nghiên cứu tài chính định lượng.